Emily Lakdawalla • Jul 04, 2014
On the masses and motions of mini-moons: Pandora's not a "shepherd," but Prometheus still is
As Cassini celebrates 10 years at Saturn, we're beginning to see its long-term observations of Saturnian moons bear fruit. I've just been looking at a couple of recent papers that use nearly a decade worth of data to try to understand the intricate motions of the ring-moons. Here's a gallery of the characters featured in this post: Pan, Daphnis, Atlas, Prometheus, Pandora, Epimetheus, Janus, and Mimas. (I posted this gallery last month, with a little more commentary on how I made it.) Mimas drives a lot of the action in Saturn's ring system, giving gravitational shoves to moonlets and ring particles alike. But I've learned from these papers that Prometheus plays a surprisingly important role, too.

The most surprising thing I've learned: You know how Prometheus and Pandora are the F ring shepherds? Prometheus on the inside, and Pandora on the outside, herding the billions of tiny particles that make up the ring into place? It's not true. Pandora is not involved in controlling the F ring's tight shape.

The first paper I looked at was written by Jeff Cuzzi and seven coauthors: "Saturn's F Ring core: Calm in the midst of chaos." (Let's pause for a moment to appreciate the quality of that paper title, which is both interesting and accurate, not boring or silly.) The paper seeks to explain why the central core of Saturn's F ring is so consistently shaped, even though various things are constantly acting to perturb it. In particular, Prometheus periodically plunges into the F ring, drawing out dramatic streamers and fans. In fact, Prometheus and Pandora, far from behaving as shepherds, actually act to stir up the motions of particles in most of the region near the F ring. Furthermore, there are other bodies that Cassini has spotted in the F ring region whose behavior is so chaotic that it's been hard to follow them; these things have "violent collisional interactions with the F ring core," so, all in all, it's really difficult to explain why the core of the F ring generally looks the same as it has ever since the Voyagers passed by.
Pretty much all of the structures in Saturn's rings that dynamicists can currently explain originate in orbital resonances, specifically mean motion resonances. Mean motion resonances are where two objects in orbit around a central body have orbit periods that are close to a ratio of two whole numbers -- like Pluto's 2:3 orbital resonance with Neptune, or the 1:2:4 orbital resonances of Ganymede, Europa, and Io.
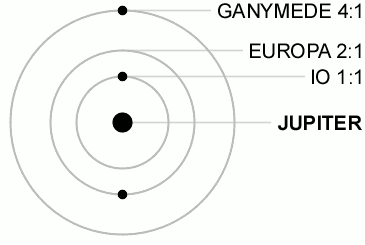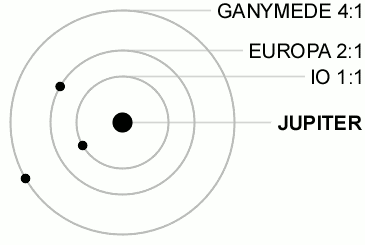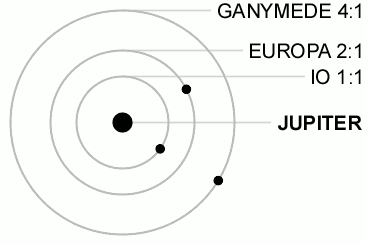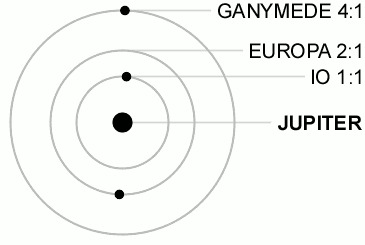
Although we think of orbital resonances using examples where objects are on stable orbits that are whole-number-ratio multiples of each other, it's actually more common for orbital resonances to be destabilizing, leaving gaps in ring systems and asteroid systems. The largest gap in Saturn's ring system -- the Cassini division -- lies where particles have 2:1 mean motion resonances with Mimas.

This much I understood already, but there are other specific kinds of resonances that I've never understood and finally I asked for help on Twitter. Both Jeff Cuzzi's paper and the one I'll be looking at next featured Lindblad resonances, which are evoked to explain spiral arm structure in galaxies, but I couldn't figure out what they were. Matt Hedman answered my call, for which I'm very grateful. He explained:
In the above simple case, the only thing that matters is where the moons are on their orbits. Things get more complicated if the orbits are eccentric or inclined, because now the moons are not just moving around the planet, they are also moving in and out and up and down. If the central planet is not just a simple point mass, then the period of time it takes from the particle to move in and out (or up and down) is not exactly the same as the time it takes for the moon to go all the way around the planet. To give an example, Saturn's moon Mimas is on an eccentric, inclined orbit. It takes Mimas 0.94242 days to go around Saturn once. However, the time it takes Mimas to move in and out once is a bit longer, 0.94490 days. This difference is why the point of Mimas' closest approach to Saturn steadily drifts (or precesses) around the planet.
You know, I've been writing about space for a long time, and I had never heard this explanation of orbital precession: that the orbital period is not the same as the "in-and-out" period. (I'm a geologist, not a physicist.) It's just a different way of framing the physics, but I had never thought of it that way before, and now a whole lot of stuff makes sense that didn't before. Eureka! Thanks, Matt. He went on:
The fact that the moon's motion has multiple periods allows for different types of resonances. In particular, a Lindblad resonance is different from the resonance illustrated in the above cartoon because the perturbation on the moon's orbit does not always come when the moon is one the same side of the planet. Instead, the moon always experiences the extra tug when it is at a particular point on its in-and-out motion.
So: consider a moon and a ring particle orbiting Saturn. We don't care (for the moment) what the orbital periods of the moon and ring particles are; what we do care about is the "in-and-out" period of the ring particle in its orbit. You have a Lindblad resonance if, every time the moon passes by the ring particle, the ring particle happens to be on the same position in its in-and-out motion. Lindblad resonances generally tend to make orbits more eccentric (make them move in and out more), and also tend to influence the position of the ring particle so that it's at either periapsis ("innest") or apoapsis ("outest") when the moon passes by. (Which one depends upon whether the particle is closer to Saturn than the moon, or farther, respectively.)
What Cuzzi and his coworkers figured out is that there is a peculiarity of the relationship between the orbital properties of Prometheus and particles in the F ring -- which they call an "antiresonance" -- where one shove from Prometheus nearly exactly cancels out the previous shove. This perfect balance is what holds the F ring particles in their orbits. Furthermore, these antiresonances are most effective in orbital positions that are not perturbed by Pandora, meaning that Pandora is not involved in shaping the F ring. "Essentially, we find that the F Ring core is not confined by a combination of Prometheus and Pandora, but a combination of Prometheus and precession." There are actually several orbital positions, about 8 kilometers apart, where Lindblad resonances and Cuzzi and company's "antiresonances" line up; it's just an accident, it seems, that the F ring lies in the particular position that it does.

The other paper, by Nick Cooper and three coauthors, has been submitted to the Astronomical Journal, and concerns "Saturn’s inner satellites: orbits, masses and the chaotic motion of Atlas from new Cassini imaging observations." (I read a preprint of the paper on arXiv.) They look at nearly nine years worth of Cassini astrometric observations to understand the motions and masses of the ringmoons. Cassini does these astrometric observations quite frequently, usually a few times per orbit. If you're a regular visitor to the Cassini raw images website, you'll see astrometric observations show up as a series of pairs of narrow-angle camera images of a dot near the rings. The two images of each moon are taken with different exposure times, helping analysts precisely locate the moon against background stars. Here is what the most recent astrometric observations of these moons look like:

There are all kinds of resonant interactions among these inner moons, many of which scientists have known about for a while. For instance, there is the way that Janus and Epimetheus have a "horseshoe" orbital configuration: on average, they orbit at the same distance from Saturn, but at any given time either Epimetheus or Janus may be closer to Saturn; once every four years, they switch positions. There is a 121:118 orbital resonance between Prometheus and Pandora, which causes their orbits to interact chaotically, making them drift in their orbits from the time of the Voyager flybys to the time of Hubble observations to the time of Cassini. Epimetheus experiences mean-motion resonances with Prometheus (15:17) and Pandora (19:21) -- but only in four of every eight years, when Epimetheus orbits closer to Saturn than Janus, not during the ensuing four years when Epimetheus is farther from Saturn than Janus. Confused yet?
You can read the paper on arXiv for a nice summary of other interesting resonances. But the passage on resonances that I found most interesting was another in which Cooper and coworkers found Prometheus to have a more important role, and Pandora a less-important one, than previously appreciated:
We show... that Atlas is currently librating in the 54:53 mean motion resonance with Prometheus....We then show that the observed short-term dynamical evolution of Atlas can be well-approximated by a three-body system consisting of Atlas, Prometheus and Saturn only, and use a chaos indicator to estimate the chaoticity in Atlas’ orbit. Hence the coupled first-order resonant interaction between Atlas and Prometheus is the primary dynamical influence on the orbit of Atlas. It follows that the primary source of chaos in the orbit of Atlas is the direct effect of the coupled resonance with Prometheus, rather than the secondary effect of the chaotic interaction between Prometheus and Pandora.
The other main result of the incredibly precise orbital motion measurements in the Cooper paper is new measurements of the masses of Atlas, Prometheus, Pandora, Janus, and Epimetheus. They find Atlas to be considerably less massive than previously estimated (by 13%); the other four were consistent with previous measurements, but the new numbers are substantially more precise.
| Solutions for GM (km3 s−2 × 10-3) | |||
|---|---|---|---|
| Satellite | Jacobson et al (2008) | Cooper et al (2014) | Mass (1012 kg) |
| Atlas | 0.44 ±0.04 | 0.384 ±0.001 | 5.76 |
| Prometheus | 10.64 ±0.10 | 10.677 ±0.006 | 160 |
| Pandora | 9.15 ±0.13 | 9.133 ±0.009 | 137 |
| Janus | 126.60 ±0.08 | 126.51 ±0.03 | 1900 |
| Epimetheus | 35.13 ±0.02 | 35.110 ±0.009 | 526 |
One final note: Cooper and coworkers reported the masses -- as is usually done -- in terms of GM, that is, the mass times the gravitational constant. They do this because the gravitational constant is an annoying number that we still haven't pinned down to nearly as high precision as physicists would like. In order to convert GM into masses, I had to look up the value of the gravitational constant, and in so doing I discovered that there was a paper published in Nature the very same day I wrote this post, with a new measurement of G. Science!
Support our core enterprises
Your support powers our mission to explore worlds, find life, and defend Earth. You make all the difference when you make a gift. Give today!
Donate

 Explore Worlds
Explore Worlds Find Life
Find Life Defend Earth
Defend Earth